四大力学都有其经典与量子相对应。经典力学对应量子力学,经典电动力学对应量子电动力学,经典统计力学对应量子统计力学,经典场论对应量子场论。唯一的例外就是经典热力学,目前通常的物理专业课程中还没有量子热力学。
在国际单位制中有7个基本单位,其中6个已能在微观的原子层面定义。唯一的例外是温度,定义它所采用的玻尔兹曼常数,或者水的相变点,是相对宏观的。我们还无法采用一个更加微观的实验手段来定义温度。
按照热力学的语言,温度反映的是分子的平均动能,而那些难以定义动能的系统,比如自旋系统,它的温度依赖性在这个定义下显得很晦涩。又或者按照能均分定理,每一个自由度贡献
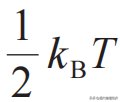
,对于较为复杂的大分子,这个定义也是失效的。系综理论将系统的温度归结为由环境来决定,但环境本身是一个相对模糊的概念,环境的温度由谁来提供,没有解释。
归根结底,熵难以被实验测定是最终的原因。因为强度量一般难以向微观推广,除了温度,压强、化学势的测定方法也相对宏观唯象。作为与温度相对应的广延量,如若熵能在微观层面被准确测定,我们就可通过能量对熵求导来获得温度。然而经典统计力学利用状态数来定义熵,令这一想法难以实施。
近年来,伴随着量子信息的迅速发展,测量纠缠熵已经不存在原则性的技术障碍。能否利用这一新技术来重新诠释热力学中的温熵关系呢?这就涉及如何在量子力学框架内重新定义热,量子热力学这一古老命题因此重焕生机。
曾经,苏联在热力学的研究中走在世界前列。在朗道的唯象理论中,自由能是热力学的核心物理量,所有系统都要向自由能最小的状态演化,正如力学系统总会选择作用量最小的运动路径一样。而自由能是温度的函数,只要能精准测量自由能,温度的确定就是题中应有之义。自由能是刻画热平衡状态的特性函数,按照导出经典涨落—耗散定理的惯例,我们应该找到一个能将平衡态与非平衡态联系起来的办法。20世纪90年代发展起来的量子涨落理论,就是在平衡态的自由能与非平衡态的不可逆功之间建立联系,从而经过测量功来确定自由能。
对于一个绝热系统,如果其能级从En跃迁到Em,则可以定义外界对其做功为W=Em-En。现若假定跃迁的初态和末态均处于热平衡状态,并且跃迁过程发生的概率分布函数为R(W),利用细致平衡原理不难推得所谓的Crooks关系[1]:

其中ΔF是末态与初态的自由能之差,R 为反向做功概率。这个关系中做功会发生涨落,因为功是与路径有关的过程量,所以如果我们对所有可能的做功路径取平均,就得到著名的Jarzynski等式[2]:
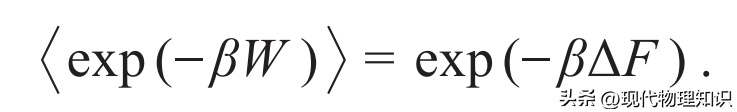
乍一看,Jarzynski等式与经典热力学中自由能与做功最小值的关系有相类似的地方,然而经典热力学的自由能需要在衡状态讨论,以确保整一个完整的过程可逆。Jarzynski等式对可逆性不做要求,任意偏离的平衡态原则上都是允许的。当然,e指数必然会放大实验测量时的误差,导致某些反向做功的路径影响更加显著。
在Jarzynski等式被提出来以前,人们更多的是采用路径积分对自由能的解决方法,也就是将温度看作虚时间,并将其作为演化的另一个维度。这跟经典热力学的定义并不自洽,因为等温—绝热过程在卡诺热机中被认为是可逆的,它无法用来定义时间之矢。如今我们在量子涨落理论的框架下,利用不一样能级状态之间相干性的变化,可以将温度之矢定义为量子系统的固有演化方向,从而为热的量子化提供新的诠释,这正是下面要谈的量子资源论的主要研究思想。
2002年发表在Science杂志上的一个工作验证了Jarzynski等式[3]。他们利用纯机械的方法将折叠的核糖核酸强行展开,经过测量施加的力来确定相应的功,并与自由能对比。此后,在蛋白质、聚合物、冷原子、离子阱等诸多实验体系中,均以不同形式验证了这一等式的合理性。作者觉得,Jarzynski等式是量子热力学一个很好的切入点,未来我们不妨用DNA或其他更具标志性的生物大分子作为测量自由能的“标准器”,并据此定义更加微观的温度,作为基本物理量使用。
自伽利略发明温度计至今,人类对于温度的研究已有四百多年,早于电、磁、光等其他学科。从热电偶到红外线,人类的测温手段日益丰富,然而横向对比其他几门学科,电已能够小到皮安,磁已能够弱到高斯,光已能够短到阿秒,而即使目前最先进的测温控温设备,其温度仍在小数点后第一位来回跳动,和四百年前几无进步。发展新的微观测温方案,我们应该全新的理论框架。
量子热力学最核心的理论体系是在量子混沌理论的基础上建立起来的,目前常见的文献中,关于量子混沌的名称通常表述为quantum chaos[4]。Berry当年曾使用quantum chaology,用以区分全量子系统的混沌效应,这个词偶尔会出现在文献中,但未广为接受。我们现在通常研究的量子混沌,是指将量子系统经典化或半经典化后的混沌,后者是指将原子核部分经典化,再与经典混沌相比较。全量子系统的混沌研究目前未有重大进展。
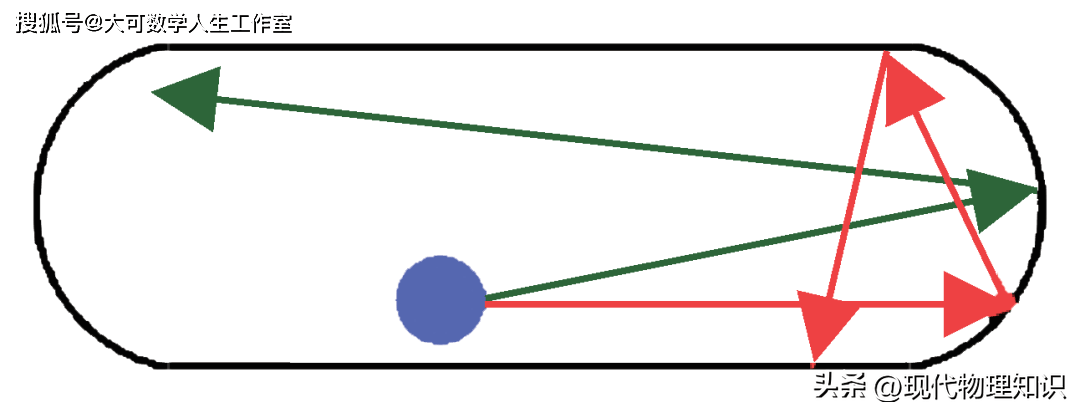
在经典力学中,与混沌相对应的概念是可积。当一个运动系统的自由度与守恒量(运动积分)的数量一致时,其运动方程是可积的(可解的)。相反,若找不出足够数量的守恒量,则该系统是混沌的。一般地讲,由于能量守恒总是先验成立,故而一维经典体系总是可积的。若再加上角动量守恒,则二维体系也可积,比如开普勒行星模型。但若二维体系有特殊的边界,比如图1所示的是混沌理论中经常作为出发点的L. A. Bunimovich体育场(stadium)模型[5],其形状如一个田径运动场,这样的一种情况下没办法找到第二个守恒量,则会出现混沌。除此以外,非微扰三体系统也因找不到足够的守恒量而成为混沌,比如水分子的三个原子、质子的三个夸克等,这是流体力学、核物理中时常发生混沌现象的原因。至于三维,不可积的情况更为常见,所以绝大多数自然系统都是混沌的,可积系统只是少数。
将这些经典混沌的概念向量子推广的研究早在van Vleck时就有了,但线年代后。Wigner等人首先用随机矩阵理论来处理量子混沌,然后是Gutzwiller等人提出迹公式(trace formula),跨出了经典混沌量子化的关键一步。1980年代以后,随着原子分子光学的发展,尤其是对电磁场中氢原子动力学行为的研究,揭示出量子混沌已经是无法回避的问题,随机矩阵与迹公式这两套理论均得以迅速发展,形成较为完整的理论体系。
(2)回归性(recurrence):无论从哪个起点出发,总能不断回到该起点;
第一条提示了要形成混沌必须有确定的势场或相互作用来约束系统的运动,排除了完全自由的系统中存在混沌的可能。第二条提示了不存在不稳定的初始状态,比如从高空抛下一个物体,从地面反弹后无法回到原位,则不是混沌的。一般人更熟悉的“蝴蝶效应”则是指第三条。在经典混沌中,一般定义
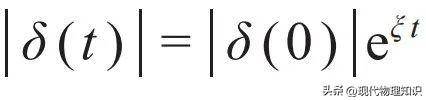
,其中δ(t)是两条起点相互接近的运动轨迹之差,ξ是Liapunov指数,它为正时就是混沌的。由于运动轨迹有界,所以δ(t)跟着时间演化并不会无限增加,而是会逐渐趋于饱和,所以为了真实反映指数敏感性,在实际计算时往往要映射到正切空间,也就是运动轨迹的导数所张成的空间。
值得一提的是,Liapunov指数是经典混沌理论的概念。在量子力学的框架下,如果波函数严格按薛定谔方程演化,即使在正切空间中也特别难看到δ(t)随e指数发散的行为。按照Ehrenfest对此的解释,需要定义一个切断时间(break time),在这一段时间内,量子体系的演化应当与经典混沌对应,反之则不存在混沌的现象。最初,切断时间被认为就是普朗克时间,但随着理解的深入,这一定义越来越不被认可。
第二种常用的鉴别混沌的指标是描述回归性的庞加莱映射。从高维的空间切出一个任意的平面,运动轨迹每穿过该平面一次,就在这个平面上打一个点。足够长时间后,规则的两体系统只会出现极少数的点,微扰的三体系统会出现一些有规律的曲线,混沌系统则会遍历整个平面,这正是用来理解各态历经的常用图像。
目前针对量子混沌的研究中,使用最多的指标是能级分布。由于可积性的差异,混沌系统的能级是互斥的(level repulsion),而可积系统则是聚簇的(level clustering)。前者的能级间距表现为高斯分布,后者表现为泊松分布,这是用来分辨量子热化态与局域态的重要指标。能级互斥正是自然界去简并倾向的体现,因此绝大多数自然系统倾向于混沌与热化,这是我们将热力学量子化的理论基础。
量子热化理论的出发点,是为量子多体系统建立一个新的吉布斯系综,通常叫做广义吉布斯系综(generalized Gibbs ensemble,GGE)。它的核心思想不再是像传统量子统计那样以某些微观粒子作为系统,而是以相空间中的一个局域空间范围作为系统,这是最核心的视角转变。在这个新视角下,能量状态的不可区分性可拿来取代微观粒子的不可区分性,从而能够在微观状态的层面重新定义热化。

在经典统计的图像中,如图2所示,要想从整个宇宙的相空间里分离出一个我们感兴趣的系统,需要把这个系统的全部自由度拿出来,就像庞加莱映射,在一个三维xyz的空间中把一整个xy截面全部抽出来,构成一个系统。咱们不可以只截取这个空间内的一个局域范围,比如一个小方块,因为它并不包含完备的自由度。然而在量子热化理论中,例如一维x方向的链,我们大家可以只抽取其中若干个格点作为系统,不用把整个一维链(x方向自由度)全部拿出来。
当我们把相空间中某个局域范围(而不是某个粒子)作为系统,剩下的范围作为环境,环境通过与系统的耦合破坏系统的某些对称性,使得系统可能到达的相空间(自由度)得以扩大,这些新自由度正是由环境提供或者映射到系统上的。反映在量子测量论中,就是环境扮演一个宏观测量者的角色,经过测量打开系统的新自由度,用数学语言来讲就是环境的某些算符与系统的哈密顿量不对易,从而不能为系统找到足够多的局域运动积分。
在此基础上,就有了ETH的基本论述[7]。ETH大体上分为两部分内容,一是对角热化假说,二是非对角热化假说。考虑一系列算符

,第一条是指,它在微正则系综中的平均值,等于其在哈密顿量不同本征态上平均值的等权重求和,即
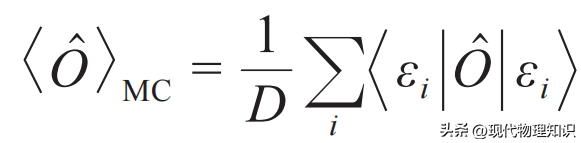
,其中εi 的取值范围是给定的能量范围[E, E+δ],D代表相应能量范围内量子态的个数。第二条是指,
的选取并不任意,而是要选择自由度较小的局域算符,一般是某个对称性不可约的产生子,从而尽可能的避免上述问题。
由于不再将单个粒子当作系统,而是将局域的空间当作系统,所以许多经典热统的观念都要有所转变。比如,经典热力学通常认为空间势能的无序度越高越容易热化,经典混沌理论也这样认为。量子热化理论则相反,空间越无序越容易局域化,从而难以热化。因此,咱们不可以再像经典混沌那样以全局的守恒量,比如能量、动量、角动量等来作为判断是否可积的标准。在量子热化理论中,即便我们能找到足够多的全局运动积分,对应于经典可积的情况下,系统仍然有很大的可能是热化的。我们要寻找的是局域运动积分(local integral of motion),它们的数量与局域状态数的关系,决定了一个系统是热化的,还是局域化的。
不同局域运动积分之间理应互相对易,比如不同格点的自旋算符总是对易的,所以整个哈密顿量未必会存在简并性。按照量子混沌理论,这应该是热化的情况。的确如此,即使存在局域运动积分,环境对系统对称性的破坏作用仍非常普适,这也是热化发生于绝大多数系统的原因。简并性的保护需要在局域运动积分的基础上,进一步引入对称性、拓扑、多体相互作用等其他因素。
ETH和经典统计中的各态历经假说究竟有什么不同?作者觉得,ETH最大的优点并不在于它描述了“绝大多数”系统的行为,而是它给出了不满足各态历经的明确条件。各态历经虽然是经典统计的基本假定,但它不同于其他物理理论,其预测性差,又难以证伪,总是会产生各种似是而非的结果。而在ETH的定义中,对于先验成立的各态历经假说,我们有了可以定量证伪它的方案,这是了不起的进步。
提到局域化一词,很容易想到的是安德森局域化。然而,赫赫有名的局域化在很久内其实都未成为显学,国内许多“固体物理”课程中,“局域化”三个字基本是一笔带过。零星的研究以导电机理为主,有不少人进入该领域是基于安德森、莫特等人的名声。基于历史传统,固体物理中研究更多的是晶体物理,用能带和能隙来区分金属、半导体和绝缘体是物理学家更习惯的思考方式,做第一性原理计算时,晶胞总是尽可能取小以减轻计算量。如图3所示,局域化的研究需要在格子模型中引入无序,破坏平移对称性,这与晶体的计算并不完全相容。由此,局域化在很久内都像是化学语言。化学家不执着于晶体,更关注无序所带来的载流子局域化,并发展出诸如极化子迁移之类的导电机理。利用Marcus理论、势能面跃迁等半经验理论,化学家在某些特定的程度上能处理好导电的量子性问题。
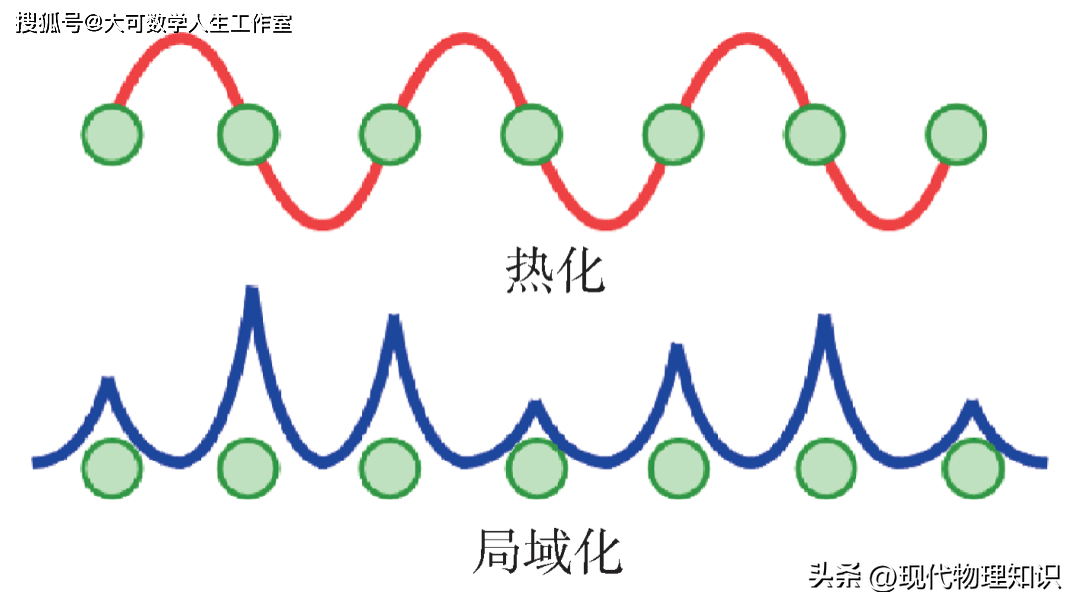
如今,局域化被提升到物质科学最本原的程度来研究,脱离了金属—绝缘体转变等具体问题的束缚,是物质科学家们对量子热化理论的回应。研究局域化的核心正是寻找量子资源,是找到推动人类进步的新材料。如果万物都会被热化,物质科学家们也要致力于找出那万分之一不会被热化的量子物质。
能带的出现是不同原子上原本简并的局域轨道在电子动能的作用下发生了去简并效应,也就是发生了热化,从而形成能级互斥。化学上,这是成键和反键轨道形成的原因。即使我们将任意杂质放进体材料中,该杂质的能级出现在能带里面,杂质轨道仍然会与母体材料中的原子轨道杂化,使我们看不清杂质和母体的区别。要想破坏热化,或形成局域化,必须要有一些非凡的物理因素出现。总结起来,可归结为如下几种情况。
第一种情况是派尔斯不稳定性,通过在一维体系中引入晶格原子微小振动,在原本的能带中劈裂出新的能隙,并在能隙内部形成隙间态,例如孤子、极化子等。一般认为,一维体系中即使再弱的无序也会导致局域化,这就是“一维体系无金属”定律。这与混沌理论自洽,因为维度越低越难以热化,即使是哈伯德模型这样平移简并的局域轨道在电子动能的作用下发生了去简并效应,也就是发生了热化,从而形成能级互斥。化学上,这是成键和反键轨道形成的原因。即使我们将任意杂质放进体材料中,该杂质的能级出现在能带里面,杂质轨道仍然会与母体材料中的原子轨道杂化,使我们看不清杂质和母体的区别。要想破坏热化,或形成局域化,必须要有一些非凡的物理因素出现。总结起来,可归结为如下几种情况。不变的系统,也只能是弱热化。
第二种情况是在三维体系中,杂质能级出现在能带外面的情况。以标准的紧束缚模型为例,考虑每个格点的在位能具有无序性,其变化的上下限为
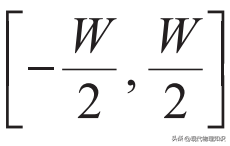
,若紧束缚模型的带宽是B,当WB时,就会有无序的能级跑到能带外面形成孤立的局域能级。
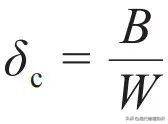
第三种情况是莫特的迁移率边(mobility edge)和变程跃迁(variablerange hopping)模型。在无序分布的在位能中,总有一些能级极为接近,但空间距离很远。这种情况下,电子不能像在通常的能带中那样正常扩散,它们会形成深入带隙的迁移率边。为了刻画变程跃迁过程,莫特给出了一个唯象的跃迁速率公式,即
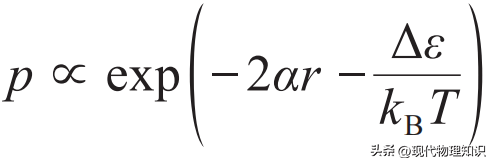
,其中r 和Δε 分别是跃迁初末态间的空间距离和能量差,α是刻画距离无序度的参数。如果我们进一步假定无序能级的能量差与体积成反比,即Δε=cr-3,c是比例系数,则最大的跃迁概率为
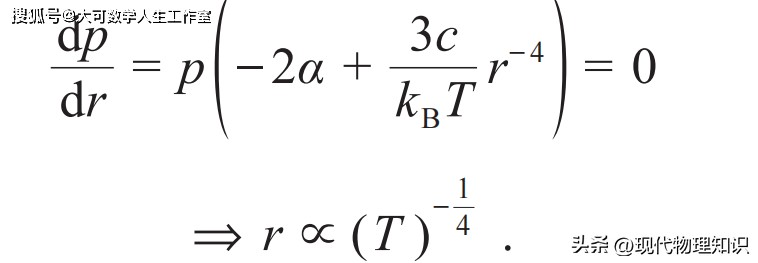
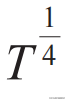
上述局域化本质上都是单电子图像,而强关联体系中由于多体相互作用的存在,一些简并性无法被去除,能级无法互斥,不再是严格意义上的量子热化态,也无法写成任何广义吉布斯系综形式的局域化,这是所谓的多体局域化(many-body localization,MBL)。这个词最早出现于2006年D. M. Basko等人发表在Annals of Physics上的文章[8]。不过早期工作仍以安德森局域化的框架为主,只是传统模型的简单推广。真正产生影响力是在量子热化理论成名以后,量子统计和凝聚态理论开始深度融合,多体局域化与量子热化成为相互对应的名词,并广泛“出圈”。
早期的多体局域化研究沿袭热化理论的习惯,主要探讨能级分布。通过建立一个多体相互作用模型,加上无序势,计算其本征能级分布是互斥的还是聚簇的,若为前者则是热化,若为后者则是多体局域化。这样做的最严重的问题,是难以与热化中的预热化、局域化中的安德森局域化相区分。随后就出现了第二类研究方案,即量子淬火动力学,淬火会导致有限尺寸的局域孤子出现,这是研究局域化非常好的出发点。在此基础上,一个完全超越预期的现象被发现,那就是纠缠熵的对数传播。
在安德森局域化中,局域态之间的相互作用是e指数衰减的,即互相之间完全隔绝,不会发生任何信息传播。但在多体局域化中,J. H. Bardarson等人的数值计算根据结果得出[9],纠缠熵会在很久内以对数形式缓慢增长。这一结果在许多计算中得以证实,被确认为多体局域化最关键的动力学特征,它反映了局域态之间有着等效长程相互作用。这是一个令人振奋的结果,意味着量子计算可以在不改变局域态布居数,也就是能量的情况下,传播量子信息。
于是,在多体局域化应用到量子计算的探讨中,有了局域比特(l-bit)的概念。所谓局域比特,其实就是局域运动积分,它们是能够长时间保持不变的局域守恒量。以经典的伊辛模型为例,它的
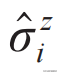
就是局域运动积分,初始状态一旦确定为它的本征态,就无法被改变。一般的,假设某个多体局域化系统的局域比特为
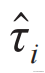
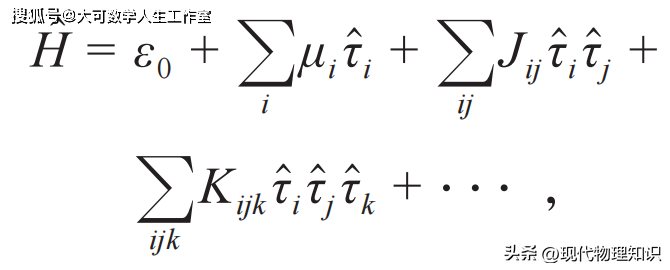
其中,ε0、μi、Jij、Kijk分别为零点能量、单体在位能、两体相互作用能、三体相互作用能。这里的局域比特可以是自旋,也可以是任意粒子或多态系统,一个实际体系的哈密顿量,只要能变换成这样的形式,它就是多体局域化的。
这样的局域比特模型能很好地解释纠缠熵的对数传播。以两个相距x的局域比特为例,
,也就是距离越远,两个局域比特退相干的时间越长。若假定纠缠熵在x范围内各态历经、均匀分布,即S∝x,立即得到S ∝ ln δt,正是纠缠熵的对数传播律。
由于离散能级和局域比特的存在,多体局域化系统的本征态必然是局域态,这些局域态一定会发生自发对称性破缺。局域比特如果是一个自旋,它只可能处在朝上或朝下的某一个态,双态之间无法转换。基态则是这些局域比特所形成的长程序,因此多体局域相也被称为本征态有序相。或许未来我们大家可以用多体局域化来统一解释强关联体系中复杂的相变问题。
当我们测量一个处于基态或热平衡状态的系统,只要这个测量手段与维持系统处于热平衡的算符不对易,系统立即进入非平衡状态。经典热力学通过涨落—耗散定理,将这一非平衡过程近似为一系列准平衡过程,从而将热与功简单联系起来。但正如Rolf Landauer那句名言:“Information is physical”,量子测量在提取信息时所消耗的能量,比经典热机的热功转换要深刻得多。正是基于这一原因,有不少人认为量子热力学就是研究量子热机的学问。
最早关于量子热机的研究从20世纪50年代就有了[10]。但那时的讨论保留了大量经典热机的特征,与现在的量子热化和局域化理论并不自洽。那时的核心任务就是将经典Otto热机量子化[11]。Otto热机即标准的四冲程内燃机,包含等容吸热、绝热做功、等容放热、绝热回复四个过程。由于量子力学不能很好地定义温度,故而Otto热机比包含等温过程的卡诺热机讨论起来更为便利。
第一步是将体积这个宏观状态,也就是将热力学第一定律推广到量子版本。对于任意微观体系的总能量,可以表示为
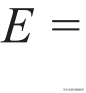
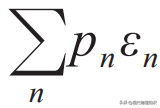
,其中pn和εn分别是第n个本征态上的布居数和本征能量。两边求微分,立即得到:
由此可见,要想在量子体系中实现等容过程,就要保持本征能谱不变,只让不同能级的布居数发生明显的变化,也就是在不同本征态之间非绝热转换。要想实现等熵(绝热)过程,则要保持布居数不变,只改变相应的本征能量。如图4所示,以一个无限深方势阱为例,初始状态时粒子处于基态,经过一个等容吸热过程,本征能量保持不变,粒子从低能级转移到高能级。然后,势阱变宽,体积变大,本征能级下降,相当于绝热过程对外做功,之后粒子经等容放热过程重新再回到基态,如此就构成了量子Otto热机工作循环。

这只是一个为了形式上与经典Otto热机对应的玩具模型,并不具备实用性,粒子无法自发推着势阱的边界往前走。真正有实用性的量子热机模型,最简单的工质是三能级系统,高温和低温热源均是单频的玻色子库。在旋转波近似下,一个玻色子库与工质之间会形成二能级系统。如果有两个玻色子库,其中一个与ε1和ε3两个能级构成二能级系统,称为高温热源,另外一个则与ε1和ε2两个能级构成二能级系统,称为低温热源。于是正反向做功的概率应正比于exp(-βh(ε3-ε1))和exp(-βl(ε2-ε1)),其中βh和βl分别为高温和低温热源的温度的倒数。若正向做功大于反向做功,则
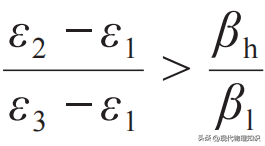
由于对热的微观认识仍不充分,即使在三能级系统这样有着明确本征能谱的系统中,对外做功过程的模拟仍存在相当大的技术难度。量子动力学无法模拟整个工作循环,甚至单次热功转换都难以模拟,所以常见做法是通过外加含时的驱动场,将能够对外做功的活性态(active state)和不能对外做功的被动态(passive state)区分开来,相当于功被三能级系统这样的工质储存起来,工质扮演了电池(battery)或飞轮(flywheel)的角色。在量子热机中,这种系统工质的作用称为功贮藏室(work repository),其中可以被提取出来的最大功被称为ergotropy,该词尚无统一中文译名。
将经典热机反向操作,就是一台吸收式制冷机(absorption refrigerator)。然而,量子制冷机并不能简单地将量子热机反向,这涉及自发对称性破缺和信息擦除的复杂问题。目前,研究者已经设计出了各种有趣的量子制冷机,比如给一个四能级系统接上三个库,其中两个扮演低温热源,另一个扮演高温热源,类似于量子光学中的双光子吸收。详细的细节内容不再赘述。
若说研究局域化是致力于破坏空间平移不变性,研究时间晶体就是破坏热力学第一定律,那么讨论量子热机的出发点就是致力于破坏热力学第二定律,也就是熵增原理。在经典热机中,熵的作用永远是负面的,拥有最高效率的理想热机一定要保持全过程可逆,熵保持不变。量子热机的本质就是要探讨将熵作为正面资源加以利用。要么是直接与能量或功相互转换,要么是以量子相干性作为催化剂(catalyst),间接促进有用功或ergotropy的增加。
这正是经典热力学中的麦克斯韦妖。常见的实现麦克斯韦妖的装置包含费曼棘轮、Lochmidt回波等。在所有可能的选项中,20世纪20年代出现的Szilárd热机最具启发性。所谓Szilárd热机,是指当一个盒子里只有一个分子时,若分子在盒子左边,让右边对外做功,当分子在右边时,让左边对外做功。由于总是真空的一边在做功,能量损耗可忽略,就等于从单一的等温环境中提取了有用功,粗看上去的确违背第二定律。
2010年,S. Toyabe等人发表在Nature Physics上的一篇文章据此设计了一个有趣的实验装置[12]。他们将两个直径为287 nm的聚苯乙烯塑料颗粒吸附在涂抹了亲和剂的玻璃衬底上,两个颗粒结合形成类二聚体结构,具有面内旋转自由度。之后将它们放置在一个精巧设计的四极电场内,通过向四个电极加入椭圆旋转的交变电场,可以让这个二聚体旋转起来。二聚体很小,它的旋转具有随机性。一直由显微镜在实时观察总系统,当某时刻二聚体所处的旋转角度正好处于电势的波峰处,就会开启一个反馈电场,让辐角反向,二聚体会因能量降低而掉到波谷中。如此反复操作,二聚体的旋转就会呈现出单向演化的特征。
这个装置看上去并没有对分子做功,与麦克斯韦妖的设想相一致。但仔细分析会发现,要实现上述操控需要对纳米颗粒的微观运动实时了解。无论是显微镜、图像识别,还是反馈电场的引入,都需要巨大的能量消耗,其作用不是让纳米颗粒运动,而仅是知道它的实时运动信息。事实上早在Szilárd热机的讨论中人们就已经明白了这一点,信息的获取本身是需要能量的,这正是Landauer那句名言要表达的含义。
物理定律的本质就是限制和约束(constraint),比如运动速度不能超过真空光速,能量不能从无到有等。所谓的资源论,就是研究怎么样对这些客观限制加以利用。量子力学更看重对称性和守恒律,所以在将热力学量子化的过程中,资源论也应当被量子化[13]。
资源论最早是2000年由D. Janzing等人引入到物理学中[14],其出发点是在当时如火如荼的冷原子技术。人们醉心于让原子的温度越来越低,但却忽视其代价。相比于单个原子,让它冷却的激光器和其他装置极其庞大,所消耗的能源难以计数。如果以冷原子实现的量子计算机当作一台量子热机,那么其效率必然极低。我们究竟能以多小的代价来冷却原子呢?寻找这个极限是量子资源论的出发点。
量子资源论之所以不沿用量子信息论的名称,主要是为了探讨信息与能量之间的转换,特别是如何将量子“相干性”作为资源来使用,而不是直接耗散掉,未来可能的工业革命非常有可能发生在对相干性这种新能量形式的使用上。传统热力学以熵或自由能作为基础物理量,它们的单向演化定义了热力学过程的不可逆性。量子资源论则要探讨,一个量子系统会自发选择怎样的演化方向,我们应该为此定义一组(不再是一个)新的物理量对其演化加以限制。
用到的数学工具就是线性代数中的完全正定保迹映射(completely positive trace-preserving map)。所谓完全正定,是指该映射作用到某算符上,作用前后该算符均是半正定的,半正定的意思就是它作用到任意态矢量上所得的内积为非负。假设某个系统S的状态用密度矩阵ρ表示,引入一个处于热平衡状态γ的环境R,使之与ρ直积并共同演化,再将环境部分求迹,即定义如下超算符:
。这个超算符称为热操作(thermal operation),它只包含量子力学中定义最良好的幺正变换和求迹操作,可以在实际物理体系中实现。热操作是完全正定保迹映射,它满足时间平移不变性并保持热平衡状态不变,这正是热力学第一和第二定律。
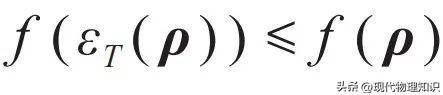
,其中f是任意可能的函数,则热操作就是一个单向操作,它在量子热力学的框架下重新定义自然演化方向。在量子资源论中用得最为广泛的函数是迹范数和相对熵。迹范数是指
,也叫量子Rényi相对熵,其中α代表熵的阶数,当0≤α≤2时,它是单调下降的。与标准的Rényi熵一样,当α→1时就是冯·诺伊曼相对熵
是环境部分随时间演化后再被求迹所产生的对系统的操作,称为Kraus算符。不失一般性,
称为滑移算符,相当于把系统的所有状态向某个能量方向挪动。很显然,滑移算符由环境的某个能量状态提供或是吸收了系统的能量所导致,
其中,ρT是热平衡分布。第二项就是经典自由能,第一项则是由量子相干性的变化导致熵变所引起的自由能变化。这里的α有很多取值,所以能有很多个不同的自由能,它们共同形成对量子体系演化方向的限制。如何将这一部分自由能加以利用,是量子资源论的重要研究课题。
其中最需要我们来关注的莫过于非对称性(asymmetry)理论。所谓非对称性,就是指ρ当中包含了
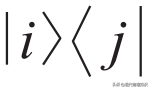
这样的在某个对称表象下的非对角元,也就是叠加态。最常见的当然就是时间平移不变性所对应的能量表象,对角元在时间演化算符作用下完全保持不变,所以叫对称态,对称态可以是纯态也可以是混态。而非对角元在时间演化时会增加一个相位,所以是破坏平移不变性的非对称态。根据热操作的单调性不难发现,最均匀的叠加态通常只能作为热操作的初态,而很难作为末态。这种难以被热操作自然演化而制备得到的非对称态,就是“昂贵的”资源,与之相反,不均匀的叠加态则是“廉价的”,能量本征态则是“免费的”。非对称性理论,能够在一定程度上帮助我们回答一个基础但悬而未决的量子力学问题:能量本征态的线性叠加态究竟是怎么样产生,又应如何被利用。此外,在非对称性理论的帮助下,我们还可以将纠缠的提纯与形成过程组成一个量子热机的循环,从而研究怎么样将量子相干性作为资源加以循环利用。
物质科学的发展历史上,无数人追寻着万物理论(theory of everything)的光芒:通过一组方程描述所有已发现的现象[15]。曾经,金兹堡—朗道理论被认为最接近这一目标。它以自由能作为判据,通过自发对称性破缺达到最终物态,不仅被成功运用于常规超导,还被普遍的应用到各种其他物态。然而随着高温超导、分数量子霍尔效应等新奇凝聚态物相的发现,这套理论体系不再普适成立[16]。量子液体、强关联、拓扑序、量子热化等一系列新理论不断被提出以解释这些新奇物性。
量子信息的发展对万物理论的探索形成了一条全新赛道。过去,人们无论研制出多么先进的表征仪器,对于物质内部微观层面发生的物理仍然需要大胆假设、小心求证。量子模拟则可以先理论后实验,通过事先设计来实现新奇物相,这是一条前所未有的研究新思路,正如Nature Physics的一篇新闻标题讲的:“Measurements make the phase”[17]。
当热力学第二定律刚被提出时,熵被认为是人类对宇宙无知的程度,后来与信息论相结合,熵也因此被赋予了信息量的物理内涵。从这个意义上讲,只要还存在熵这个物理量,万物理论似乎就不应该存在。但是现在,纠缠熵作为一个可观测量已经渗透到物质科学研究的方方面面,基于纠缠的理论非常有可能在未来扮演万物理论的角色。在那之前,关于热的定义是否还应当与熵挂钩,需要更加仔细研究。
不仅是热,粒子数是否一个多余的概念?化学势与温度是否同一个物理量?这一类问题近年来也被广泛探讨[18]。随着拓扑弦等图像逐渐将基本粒子囊括进纠缠的理论体系中,这样的探讨会更加深入,并逐渐建立起真正具有量子化特征的热力学理论,那也将是更具革命性的万物理论。